Module: Region Similarity#
Assuming that transcripts are homogeneously distributed throughout the cell, we expect there to be similar expression of genes in the nucleus and in the rest of the cell. If this is not the case, it can be indicative of transcript spillover from adjacent cells.
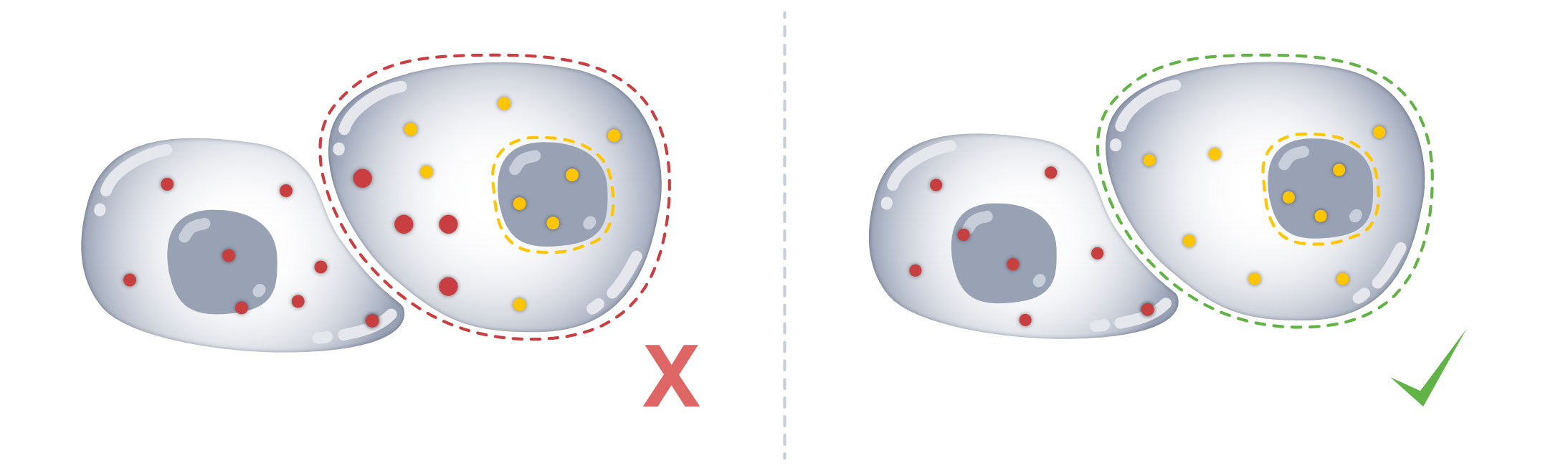
The region similarity (rs) module provides metrics to assess how similar the expression profiles are between subcellular regions (e.g., cell and nucleus).
To follow along with this tutorial, you can download the data from here.
[1]:
%load_ext autoreload
%autoreload 2
[2]:
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import spatialdata as sd
import spatialdata_plot # noqa
from scipy.stats import linregress
import segtraq
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/.venv/lib/python3.13/site-packages/spatialdata/_core/query/relational_query.py:531: FutureWarning: functools.partial will be a method descriptor in future Python versions; wrap it in enum.member() if you want to preserve the old behavior
left = partial(_left_join_spatialelement_table)
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/.venv/lib/python3.13/site-packages/spatialdata/_core/query/relational_query.py:532: FutureWarning: functools.partial will be a method descriptor in future Python versions; wrap it in enum.member() if you want to preserve the old behavior
left_exclusive = partial(_left_exclusive_join_spatialelement_table)
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/.venv/lib/python3.13/site-packages/spatialdata/_core/query/relational_query.py:533: FutureWarning: functools.partial will be a method descriptor in future Python versions; wrap it in enum.member() if you want to preserve the old behavior
inner = partial(_inner_join_spatialelement_table)
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/.venv/lib/python3.13/site-packages/spatialdata/_core/query/relational_query.py:534: FutureWarning: functools.partial will be a method descriptor in future Python versions; wrap it in enum.member() if you want to preserve the old behavior
right = partial(_right_join_spatialelement_table)
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/.venv/lib/python3.13/site-packages/spatialdata/_core/query/relational_query.py:535: FutureWarning: functools.partial will be a method descriptor in future Python versions; wrap it in enum.member() if you want to preserve the old behavior
right_exclusive = partial(_right_exclusive_join_spatialelement_table)
We start out by loading the data into a SegTraQ object.
[3]:
# loading the spatialdata object
sdata = sd.read_zarr("../../data/xenium_v1_data/sdata_proseg_v3_crop.zarr")
# putting the object into a SegTraQ object
st = segtraq.SegTraQ(
sdata,
points_cell_id_key="assignment",
points_background_id=None,
points_gene_key="gene",
tables_area_key=None,
tables_cell_id_key="cell",
shapes_cell_id_key="cell",
tables_centroid_x_key="centroid_x",
tables_centroid_y_key="centroid_y",
)
sdata
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/src/segtraq/SegTraQ.py:130: RuntimeWarning: No area column specified for tables. Area will be automatically computed from shapes.
validate_spatialdata(
/g/huber/users/meyerben/notebooks/spatial_transcriptomics/SegTraQ/src/segtraq/bl/baseline.py:564: UserWarning: Geometry is in a geographic CRS. Results from 'area' are likely incorrect. Use 'GeoSeries.to_crs()' to re-project geometries to a projected CRS before this operation.
areas = geom.area.values
[3]:
SpatialData object, with associated Zarr store: /g/huber/projects/CODEX/segtraq/data/20260204_SegTraQ_sdata/xenium_v1_data/sdata_proseg_v3_crop.zarr
├── Images
│ └── 'morphology_focus': DataTree[cyx] (1, 2500, 2500), (1, 1250, 1250), (1, 625, 625), (1, 313, 313), (1, 156, 156)
├── Points
│ └── 'transcripts': DataFrame with shape: (<Delayed>, 10) (3D points)
├── Shapes
│ ├── 'cell_boundaries': GeoDataFrame shape: (1533, 1) (2D shapes)
│ ├── 'cell_boundaries_z0': GeoDataFrame shape: (1518, 2) (2D shapes)
│ ├── 'cell_boundaries_z1': GeoDataFrame shape: (1520, 2) (2D shapes)
│ ├── 'cell_boundaries_z2': GeoDataFrame shape: (1507, 2) (2D shapes)
│ ├── 'cell_boundaries_z3': GeoDataFrame shape: (1305, 2) (2D shapes)
│ └── 'nucleus_boundaries': GeoDataFrame shape: (1501, 1) (2D shapes)
└── Tables
└── 'table': AnnData (1533, 480)
with coordinate systems:
▸ 'global', with elements:
morphology_focus (Images), transcripts (Points), cell_boundaries (Shapes), cell_boundaries_z0 (Shapes), cell_boundaries_z1 (Shapes), cell_boundaries_z2 (Shapes), cell_boundaries_z3 (Shapes), nucleus_boundaries (Shapes)
As you can see, the spatialdatadataset contains cell and nuclear masks as shapes. It is important that you have a nuclear segmentation in your object, otherwise you will not be able to compute the metrics below.
Intersection over Union between cell and nucleus masks#
First, we get the nucleus that overlaps most with each cell and compute the Intersection over Union (IoU) between cell and nuclear masks using the method match_nuclei_to_cells().
[4]:
results_df = st.rs.match_nuclei_to_cells()
results_df.head()
[4]:
| cell | nucleus_id | iou | nucleus_fraction | |
|---|---|---|---|---|
| 0 | 70066 | 78094.0 | 0.372469 | 0.909792 |
| 1 | 70067 | NaN | NaN | NaN |
| 2 | 70069 | 78081.0 | 0.621191 | 0.938538 |
| 3 | 70070 | 78084.0 | 0.357129 | 0.969828 |
| 4 | 70071 | 78083.0 | 0.662761 | 0.994992 |
For each cell_id, we obtain the ID (nucleus_id) of the nucleus mask with the highest IoU. If a cell does not overlap with any nucleus, the function returns a missing value for nucleus_id. In addition to the IoU, we also report the fraction of the nucleus that overlaps with the cell. If the nucleus has an invalid geometry, IoU and nucleus_fraction are reported as NA.
Let’s see what this looks like when we plot the IoU spatially.
[5]:
# link annotations with cell boundaries
sdata.tables["table"].obs["region"] = "cell_boundaries"
sdata.set_table_annotates_spatialelement("table", region="cell_boundaries")
# plot
sdata.pl.render_shapes(
element="cell_boundaries",
color="iou",
cmap="viridis",
fill_alpha=0.5,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.render_shapes(
element="nucleus_boundaries",
fill_alpha=0.2,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(title="Overlay of nuclei and cell masks colored by IoU", colorbar=True)
WARNING Found 35 NaN values in color data. These observations will be colored with the 'na_color'.
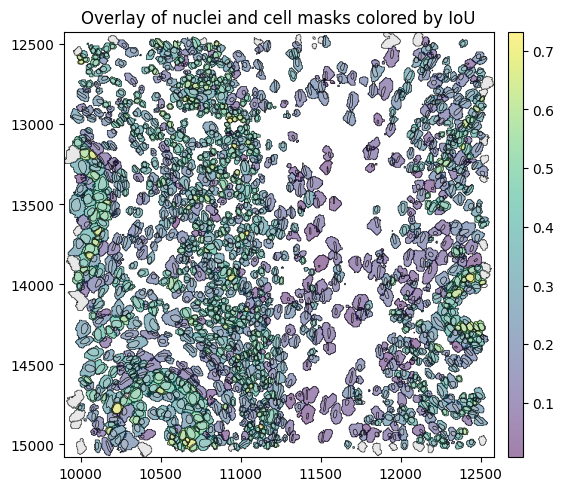
We will quickly set up some helper functions to facilitate plotting.
[6]:
# helper functions for plotting
def plot_histogram(
df,
column,
bins=30,
figsize=(6, 5),
color="steelblue",
edgecolor="black",
show_median=True,
median_kwargs=None,
median_color="red",
title=None,
xlabel=None,
ylabel="Count",
ax=None,
):
values = df[column].dropna()
median_value = np.median(values)
if ax is None:
fig, ax = plt.subplots(figsize=figsize, constrained_layout=True)
ax.hist(values, bins=bins, color=color, edgecolor=edgecolor)
if show_median:
median_kwargs = median_kwargs or {}
ax.axvline(
median_value,
linestyle="--",
linewidth=2,
color=median_color,
label=f"Median = {median_value:.2f}",
**median_kwargs,
)
ax.legend()
ax.set_title(title or f"Distribution of {column}")
ax.set_xlabel(xlabel or column)
ax.set_ylabel(ylabel)
plt.show()
def plot_regression(
df,
x,
y,
figsize=(6, 6),
dropna=True,
ci=95,
scatter_kws=None,
line_kws=None,
title=None,
xlabel=None,
ylabel=None,
r2_loc=(0.05, 0.95),
r2_fmt="{:.3f}",
ax=None,
):
data = df[[x, y]]
if dropna:
data = data.dropna()
# Regression stats
slope, intercept, r_value, p_value, std_err = linregress(data[x], data[y])
r_squared = r_value**2
if ax is None:
fig, ax = plt.subplots(figsize=figsize, constrained_layout=True)
scatter_kws = scatter_kws or {"alpha": 0.6}
line_kws = line_kws or {"color": "red"}
sns.regplot(
data=data,
x=x,
y=y,
ci=ci,
scatter_kws=scatter_kws,
line_kws=line_kws,
ax=ax,
)
# R² annotation
ax.text(
r2_loc[0],
r2_loc[1],
rf"$R^2 = {r2_fmt.format(r_squared)}$",
transform=ax.transAxes,
verticalalignment="top",
fontsize=12,
bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.8),
)
ax.set_xlabel(xlabel or x)
ax.set_ylabel(ylabel or y)
ax.set_title(title or f"{y} vs. {x}")
ax.grid(True)
plt.show()
We can now investigate what the distribution of IoUs looks like.
[7]:
plot_histogram(
df=sdata["table"].obs,
column="iou",
xlabel="Intersection over Union (IoU)",
)
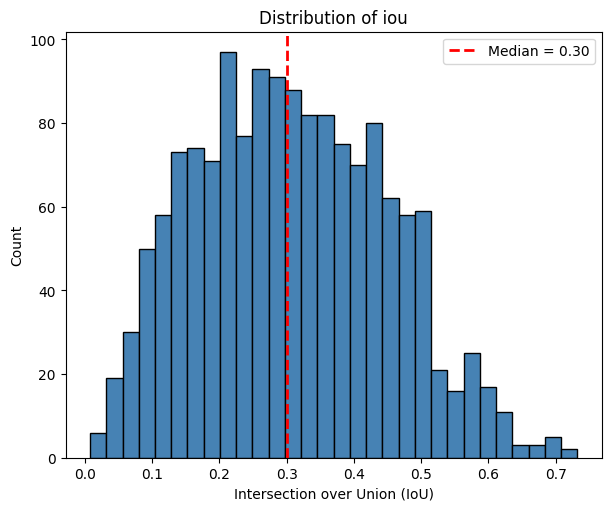
Expression similarity between cell and nucleus#
Now that we have matched each cell with a nucleus, we can investigate how similar the expression profiles are between the nucleus and the whole cell (including the nucleus). For this, we use the function similarity_nucleus_cell().
[8]:
similarity_df = st.rs.similarity_nucleus_cell(metric="cosine_sim")
[9]:
plot_histogram(
df=sdata["table"].obs,
column="similarity_nucleus_cell",
title="Cosine similarity between cell and nucleus expression",
xlabel="Cosine similarity",
)
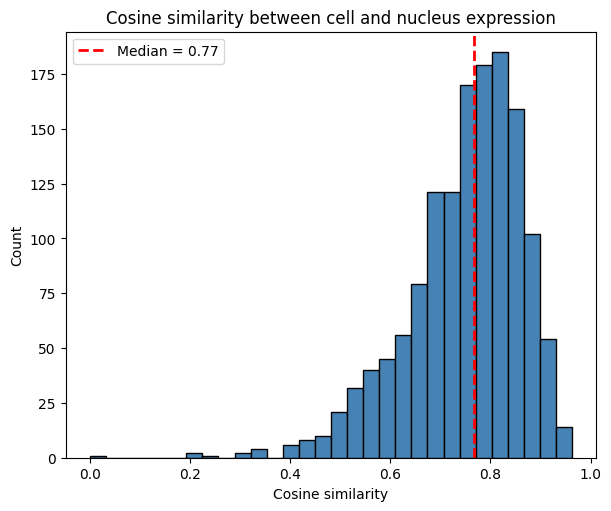
The histogram shows the distribution of cosine similarity values across cells. It is right-skewed, with a median of 0.77. This provides intuition about possible spatial spillover: cells may be contaminated by neighboring cells, assuming that nuclei capture expression with less contamination due to their smaller radius.
[10]:
plot_regression(
df=sdata["table"].obs,
x="iou",
y="similarity_nucleus_cell",
title="Cosine sim. vs. IoU with Regression Line",
ylabel="Cosine similarity between cell and nucleus intersection",
)
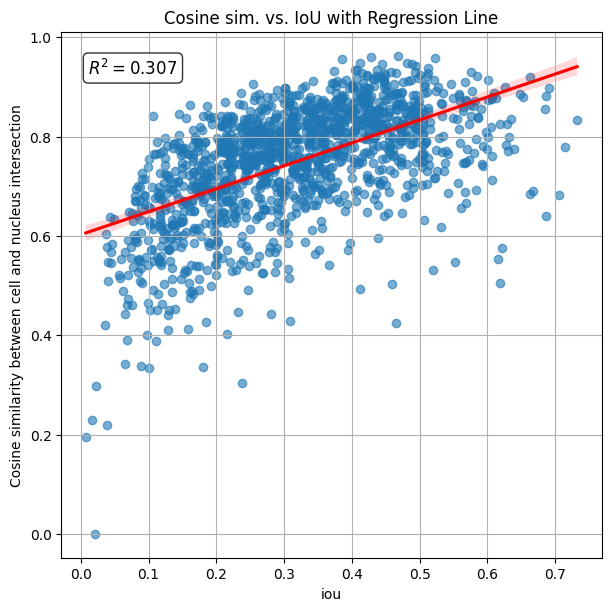
The calculated R2 (coefficient of determination) is 0.307, indicating that similarity/correlation between cell and nucleus increases with their IoU.
The spatial plot below shows cell boundaries colored by cosine similarity between the nucleus and the cell. Cells whose transcripts are distributed across the nucleus region tend to have higher similarity with the nucleus, while cells whose transcripts are located outside the nuclear region —potentially due to spillover from neighboring cells— tend to exhibit lower similarity.
[11]:
# link annotations with cell boundaries
sdata.tables["table"].obs["region"] = "cell_boundaries"
sdata.set_table_annotates_spatialelement("table", region="cell_boundaries")
# plot
fig, ax = plt.subplots(1, 2, figsize=(10, 5), constrained_layout=True)
sdata.pl.render_shapes(
element="cell_boundaries",
color="iou",
cmap="viridis",
fill_alpha=1.0,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(ax=ax[0], title="Overlay of nuclei and cell masks colored by IoU", colorbar=True)
sdata.pl.render_shapes(
element="cell_boundaries",
color="similarity_nucleus_cell",
cmap="viridis",
fill_alpha=1.0,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(ax=ax[1], title="Overlay of nuclei and cell masks colored by cosine similarity", colorbar=True)
WARNING Found 35 NaN values in color data. These observations will be colored with the 'na_color'.
WARNING Found 121 NaN values in color data. These observations will be colored with the 'na_color'.
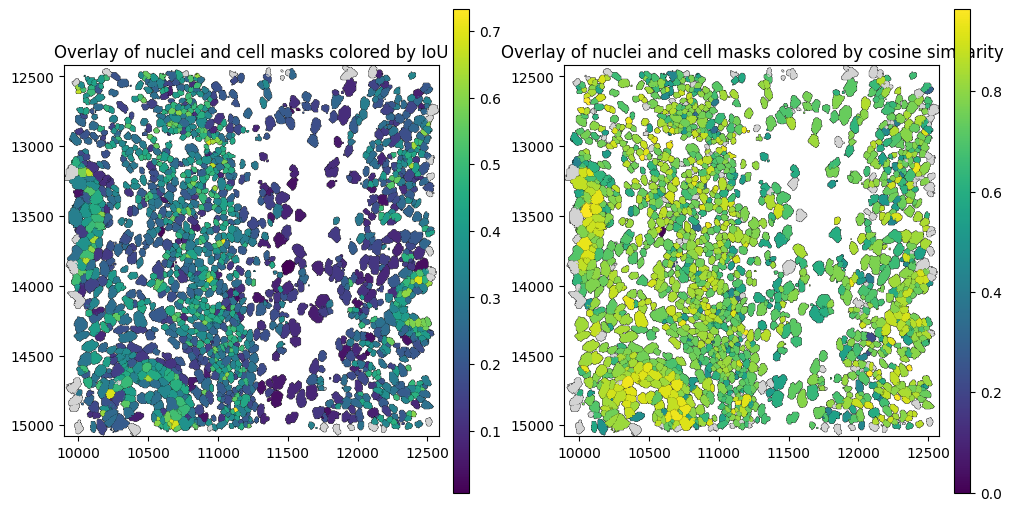
Let’s have a look at some cells witha low IoU, but a high similarity between the nucleus and the whole cell.
[12]:
obs = sdata["table"].obs
df = obs[["cell", "iou", "similarity_nucleus_cell"]].dropna()
df.loc[df["iou"] < 0.1].sort_values("similarity_nucleus_cell", ascending=False).head()
[12]:
| cell | iou | similarity_nucleus_cell | |
|---|---|---|---|
| 70961 | 70961 | 0.099841 | 0.738821 |
| 75471 | 75471 | 0.091001 | 0.727011 |
| 71219 | 71219 | 0.095490 | 0.714954 |
| 70949 | 70949 | 0.090434 | 0.713838 |
| 72782 | 72782 | 0.084363 | 0.700521 |
We can see that there are some cells with high similarity_nucleus_cell despite low IoU. Let’s investigate one of these cells in more detail. By plotting the cell (centroid marked by grey cross) with its nucleus (centroid marked by black cross) and assigned transcripts (red), we can see that for this cell, the nucleus is small in comparison to the cell, however the transcripts are still somewhat homogeneously distributed within the cell, leading to the high similarity.
[13]:
cid = (
df.loc[df["iou"] < 0.1]
.dropna(subset=["similarity_nucleus_cell"])
.sort_values("similarity_nucleus_cell", ascending=False)
.iloc[0]["cell"]
)
cid
[13]:
np.float64(70961.0)
[14]:
# helper function for plotting
def plot_cell_with_nucleus_and_transcripts(
cid: float | int,
title: str,
pix_to_um_scale_factor: float = 0.2125,
repositioned_transcripts: bool = False,
padding=200,
genes=None,
center_layer="nucleus_boundaries",
outer_layer="cell_boundaries",
):
# add annotation of this cell to .obs
sdata["table"].obs["focal_cell"] = sdata["table"].obs.index == cid
# compute x,y of cell and nucleus centroids in µm space
centroid_x_cell_px = sdata["cell_boundaries"].loc[cid].geometry.centroid.x
centroid_y_cell_px = sdata["cell_boundaries"].loc[cid].geometry.centroid.y
centroid_x_cell = centroid_x_cell_px / pix_to_um_scale_factor
centroid_y_cell = centroid_y_cell_px / pix_to_um_scale_factor
nid = sdata["table"].obs.loc[sdata["table"].obs["cell"] == cid, "nucleus_id"]
centroid_x_nucleus = sdata["nucleus_boundaries"].loc[nid].geometry.centroid.x / pix_to_um_scale_factor
centroid_y_nucleus = sdata["nucleus_boundaries"].loc[nid].geometry.centroid.y / pix_to_um_scale_factor
# add annotation of this cell to .points and build new `PointsModel``
trans = sdata.points["transcripts"].compute()
trans["focal_cell"] = "other_cells"
trans.loc[trans["assignment"] == cid, "focal_cell"] = "focal_cell"
trans["focal_cell"] = trans["focal_cell"].astype("category")
if repositioned_transcripts:
trans = trans.drop(columns=["x", "y", "z"])
trans = trans.rename(columns={"repositioned_x": "x", "repositioned_y": "y", "repositioned_z": "z"})
sdata.points["transcripts_2"] = sd.models.PointsModel.parse(trans)
T = sd.transformations.get_transformation(sdata.points["transcripts"])
sd.transformations.set_transformation(sdata.points["transcripts_2"], T)
# zoom in for better visibility
sdata_cropped = sdata.query.bounding_box(
axes=["x", "y"],
min_coordinate=[centroid_x_cell - padding, centroid_y_cell - padding],
max_coordinate=[centroid_x_cell + padding, centroid_y_cell + padding],
target_coordinate_system="global",
)
# plot cell and transcripts of that cell
axes = plt.subplots(1, 1, figsize=(8, 8), constrained_layout=True)[1]
plot = sdata_cropped.pl.render_shapes(
element=center_layer,
fill_alpha=0.2,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.render_shapes(
element=outer_layer,
color="focal_cell",
fill_alpha=0.1,
outline_alpha=1.0,
outline_width=0.5,
outline_color="blue",
)
if genes is None:
plot = plot.pl.render_points(
"transcripts_2",
color="focal_cell",
fill_alpha=0.1,
groups=["focal_cell"],
palette=["red"],
)
else:
plot = plot.pl.render_points(
"transcripts",
color="gene",
fill_alpha=0.1,
groups=genes,
palette=["red"],
)
plot.pl.show(
ax=axes,
title=title,
colorbar=True,
)
# landmark for cell and nucleus centroid
axes.scatter([centroid_x_cell], [centroid_y_cell], marker="+", s=400, c="black", linewidths=2, zorder=10, alpha=0.4)
axes.scatter([centroid_x_nucleus], [centroid_y_nucleus], marker="+", s=400, c="black", linewidths=2, zorder=10)
[15]:
plot_cell_with_nucleus_and_transcripts(cid, title="Cell with high similarity_nucleus_cell despite high IoU")
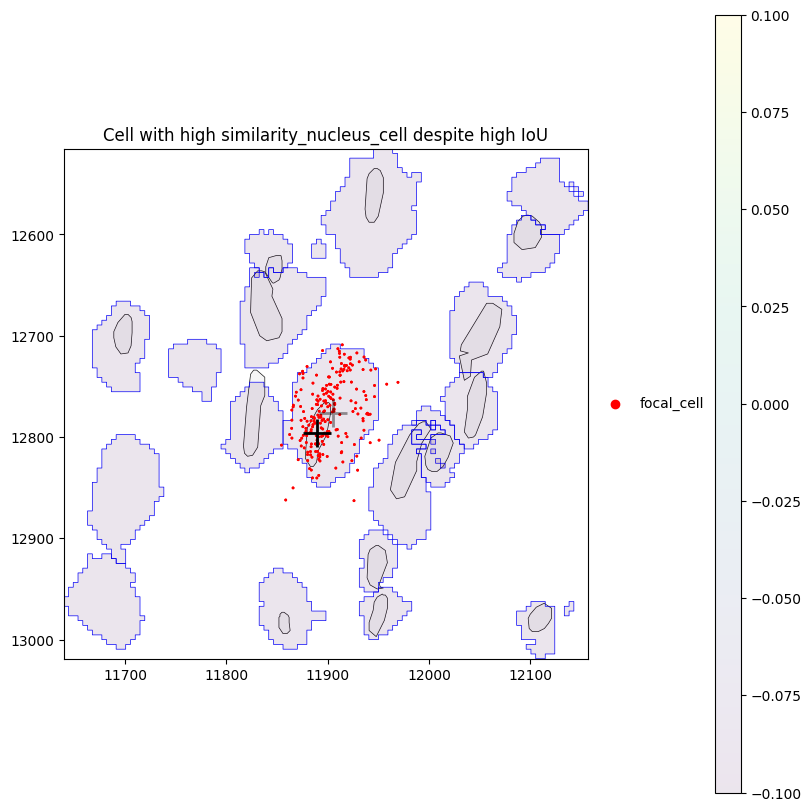
Instead of the true (raw) coordinates, we can also plot the repositioned coordinates of transcripts, which shows that proseg places them inside the cell.
[16]:
plot_cell_with_nucleus_and_transcripts(cid, repositioned_transcripts=True, title="Repositioned transcripts")
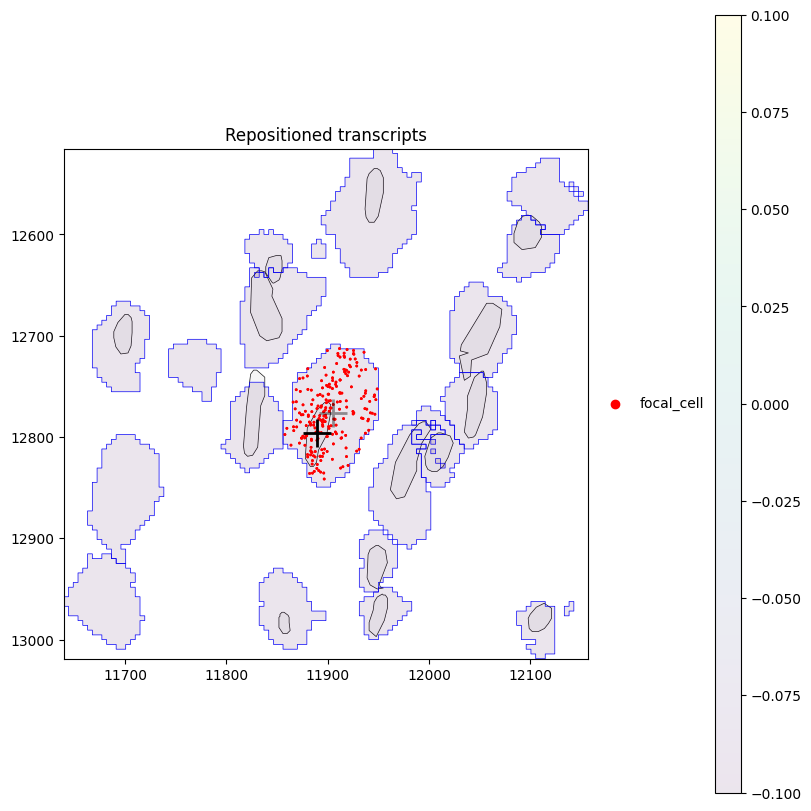
Such cells can be identified easily via the metric pct_outside_cell, which comptues the percentage of transcripts that are assigned to a cell, but localized outside its border.
[17]:
st.ps.percentage_transcripts_in_compartments().head()
[17]:
| n_total_all_genes | n_outside_cell_all_genes | n_in_nucleus_overlap_all_genes | n_in_cytoplasm_all_genes | pct_outside_cell_all_genes | pct_nucleus_all_genes | pct_cytoplasm_all_genes | |
|---|---|---|---|---|---|---|---|
| assignment | |||||||
| 70066.0 | 16 | 5 | 6 | 5 | 31.250000 | 37.500000 | 31.250000 |
| 70067.0 | 5 | 2 | 0 | 3 | 40.000000 | 0.000000 | 60.000000 |
| 70069.0 | 31 | 10 | 11 | 10 | 32.258065 | 35.483871 | 32.258065 |
| 70070.0 | 86 | 14 | 31 | 41 | 16.279070 | 36.046512 | 47.674419 |
| 70071.0 | 34 | 12 | 19 | 3 | 35.294118 | 55.882353 | 8.823529 |
So, just looking at the similarity between the nucleus and the entire cell isn’t specific enough. As a better metric, we therefore compute the similarity between the transcripts in the cell region intersecting the nucleus and the transcripts in the remaining cell region (we call this the cytoplasm, however with Proseg, this can also include transcripts that were originally measured outside of the cell, as shown above).
Similarity between Nucleus and Cytoplasm#
The function similarity_nucleus_cytoplasm() computes the cosine similarity between the spatial transcript feature counts within the nucleus and the cytoplasm. It is applicable only when nuclear masks are available. It returns NaN when the regions have no or not a sufficient number of overlapping transcripts (min_transcripts, min_genes). A low correlation/similarity may indicate that the cell boundary extension captures neighborhood or ambient signal rather than true intracellular
expression—a concern similarly highlighted by segmentation benchmarks such as Baysor. This is based on the assumption that transcripts are homogeneously distributed within the cell and not localized in specific subcellular regions.
[18]:
sim_nuc_cyto_df = st.rs.similarity_nucleus_cytoplasm()
sim_nuc_cyto_df.head()
[18]:
| cell | nucleus_id | iou | nucleus_fraction | similarity_nucleus_cytoplasm | |
|---|---|---|---|---|---|
| 0 | 70066 | 78094.0 | 0.372469 | 0.909792 | NaN |
| 1 | 70067 | NaN | NaN | NaN | NaN |
| 2 | 70069 | 78081.0 | 0.621191 | 0.938538 | NaN |
| 3 | 70070 | 78084.0 | 0.357129 | 0.969828 | 0.547531 |
| 4 | 70071 | 78083.0 | 0.662761 | 0.994992 | NaN |
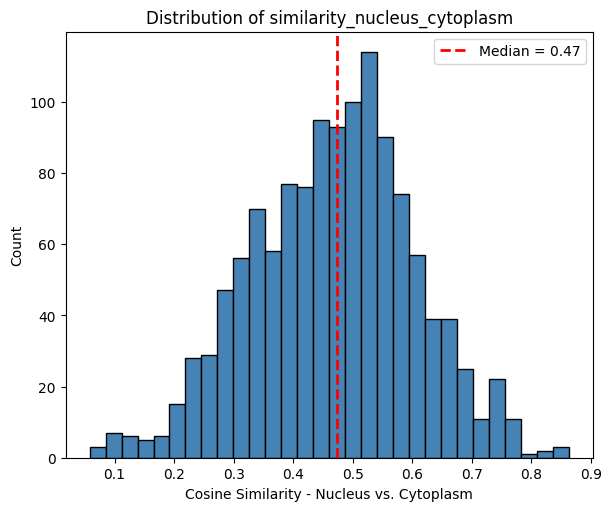
The histogram below shows that the cosine similarity between the nucleus and remaining part of the cell is 0.47.
[19]:
plot_histogram(
df=sdata["table"].obs,
column="similarity_nucleus_cytoplasm",
xlabel="Cosine Similarity - Nucleus vs. Cytoplasm",
)
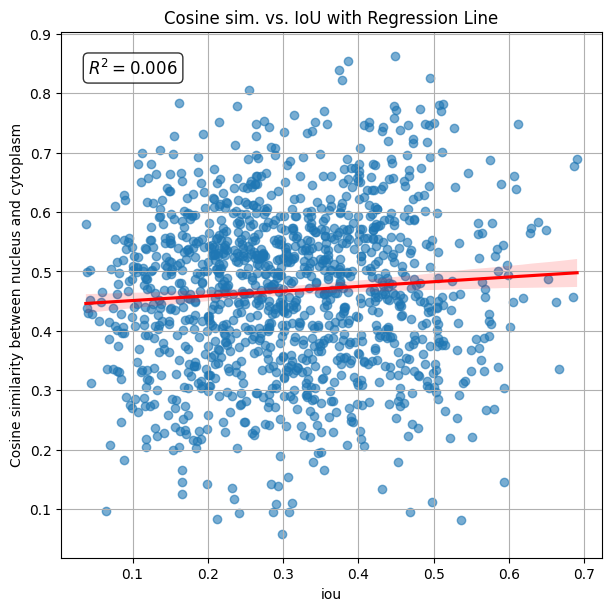
The scatter plot below visualizes the cosine similarity between transcript counts in the intersection and remainder of each cell, plotted against the Intersection over Union (IoU) with the nucleus. The calculated R2 value is 0.006, indicating that similarity_nucleus_cytoplasm is independent of IoU.
[20]:
plot_regression(
df=sdata["table"].obs,
x="iou",
y="similarity_nucleus_cytoplasm",
title="Cosine sim. vs. IoU with Regression Line",
ylabel="Cosine similarity between nucleus and cytoplasm",
)
The spatial plots below shows the spatial distribution of computed correlations. The cosine similarity between parts can be a measure of how much neighboring signal is captured.
[21]:
# link annotations with cell boundaries
sdata.tables["table"].obs["region"] = "cell_boundaries"
sdata.set_table_annotates_spatialelement("table", region="cell_boundaries")
axes = plt.subplots(1, 3, figsize=(16, 6), constrained_layout=True)[1].flatten()
sdata.pl.render_shapes(
element="nucleus_boundaries",
fill_alpha=0.2,
outline_width=0.5,
outline_alpha=1.0,
outline_color="black",
).pl.render_shapes(
element="cell_boundaries",
color="iou",
cmap="viridis",
fill_alpha=0.5,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(
ax=axes[0],
title="Intersection over Union (IoU)",
colorbar=True,
figsize=(6, 6),
)
sdata.pl.render_shapes(
element="nucleus_boundaries",
fill_alpha=0.2,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.render_shapes(
element="cell_boundaries",
color="similarity_nucleus_cell",
cmap="viridis",
fill_alpha=0.5,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(
ax=axes[1],
title="Nucleus vs. whole cell",
colorbar=True,
figsize=(6, 6),
)
sdata.pl.render_shapes(
element="nucleus_boundaries",
fill_alpha=0.2,
outline_width=0.5,
outline_alpha=1.0,
outline_color="black",
).pl.render_shapes(
element="cell_boundaries",
color="similarity_nucleus_cytoplasm",
cmap="viridis",
fill_alpha=0.5,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(
ax=axes[2],
title="Nucleus vs. cytoplasm",
colorbar=True,
figsize=(6, 6),
)
WARNING Found 35 NaN values in color data. These observations will be colored with the 'na_color'.
WARNING Found 121 NaN values in color data. These observations will be colored with the 'na_color'.
WARNING Found 274 NaN values in color data. These observations will be colored with the 'na_color'.
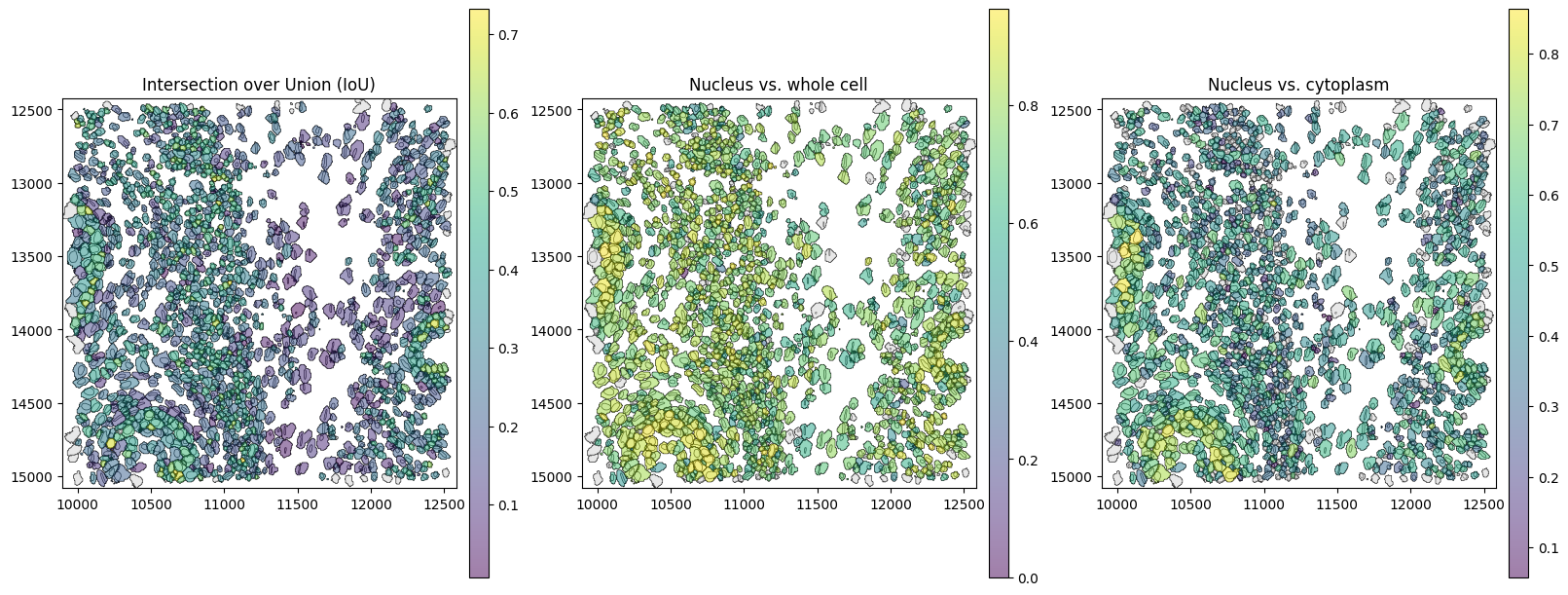
Above, we can see that there are some cells with low cosine similarity between parts despite high IoU. Let’s investigate these. This happens when the transcripts of a gene are only localized in the nucleus but not in the cytoplasm or vice versa.
[22]:
obs = sdata.tables["table"].obs
cid = (
obs.loc[obs["iou"] > 0.65]
.dropna(subset=["similarity_nucleus_cytoplasm"])
.sort_values("similarity_nucleus_cytoplasm")
.iloc[0]["cell"]
)
cid
[22]:
np.uint32(70882)
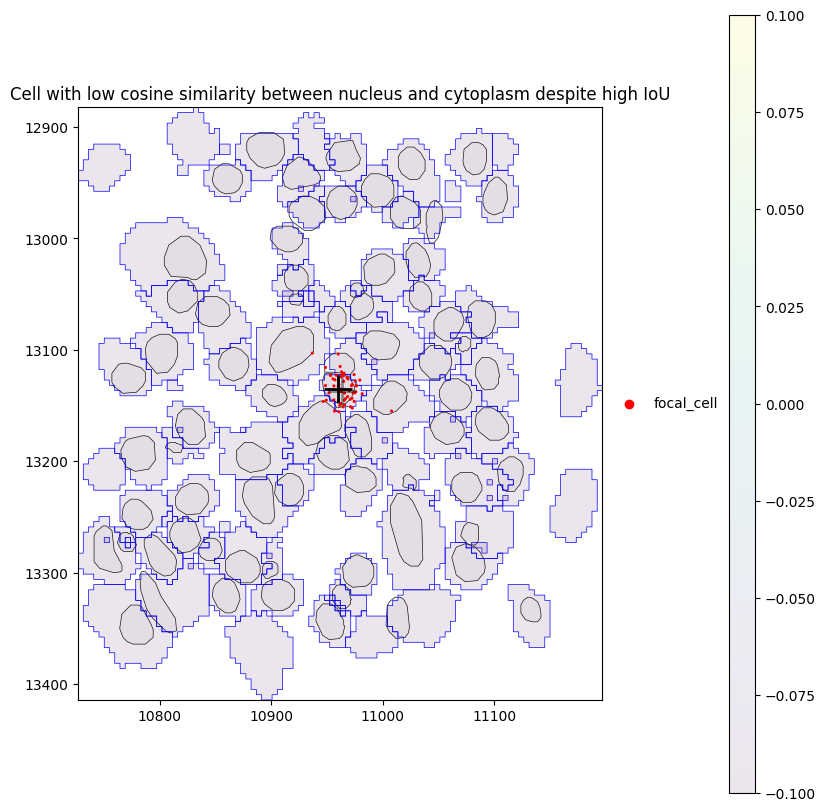
[23]:
plot_cell_with_nucleus_and_transcripts(
cid, title="Cell with low cosine similarity between nucleus and cytoplasm despite high IoU"
)
Similarity between the cell border with its neigbhorhood#
The function similarity_nucleus_cytoplasm() computes the cosine similarity between (1) the cell border and an eroded interior and (2) the cell border and the immediate neighborhood.
Specifically, the function:
Erodes each cell polygon to obtain a center region.
Defines the border region as the set difference between the full cell and its eroded center.
Computes gene expression profiles for center and border.
Computes the correlation between center and border expression.
Computes the correlation between border expression and the neighborhood expression profile.
The ratio of the latter two
[24]:
border_nhood_df = st.rs.similarity_border_neighborhood()
[25]:
border_nhood_df.head()
[25]:
| cell | similarity_center_border | similarity_border_neighborhood | ratio_border_neighborhood_to_center | |
|---|---|---|---|---|
| 0 | 70069 | 0.489025 | 0.276086 | 0.564564 |
| 1 | 70070 | 0.394818 | 0.179005 | 0.453386 |
| 2 | 70072 | 0.480105 | 0.481392 | 1.002680 |
| 3 | 70073 | 0.559856 | 0.380872 | 0.680304 |
| 4 | 70074 | 0.440363 | 0.355462 | 0.807202 |
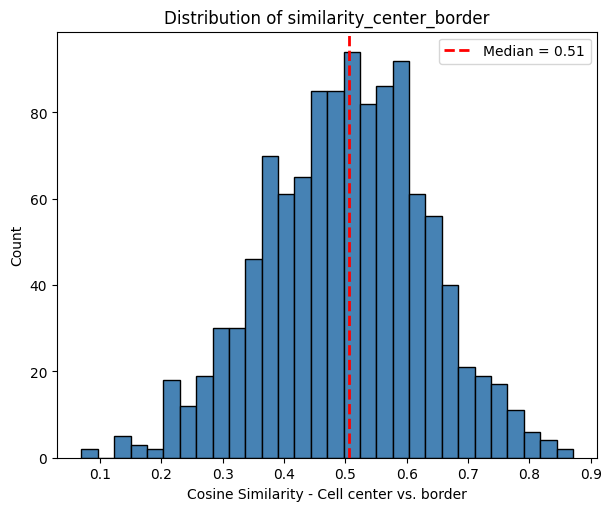
The histogram below shows the distribution of the correlation between the cell center and border.
[26]:
plot_histogram(
df=sdata["table"].obs,
column="similarity_center_border",
xlabel="Cosine Similarity - Cell center vs. border",
)
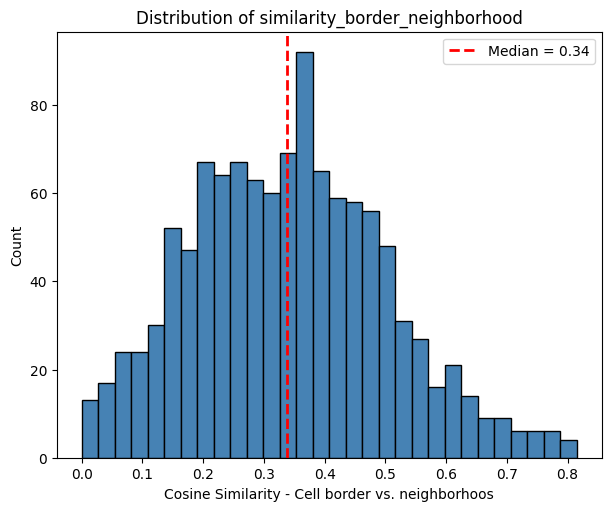
The histogram below shows the distribution of the correlation between the cell border and its neigbhorhood (with a distance of twice cell radius from its centroid). As expected, the correlation to the cell center is higher than to the cell neighborhood. This will differ depending on whether the cell is located within a homogeneous or a heterogeneous neighborhood.
[27]:
plot_histogram(
df=sdata["table"].obs,
column="similarity_border_neighborhood",
xlabel="Cosine Similarity - Cell border vs. neighborhoos",
)
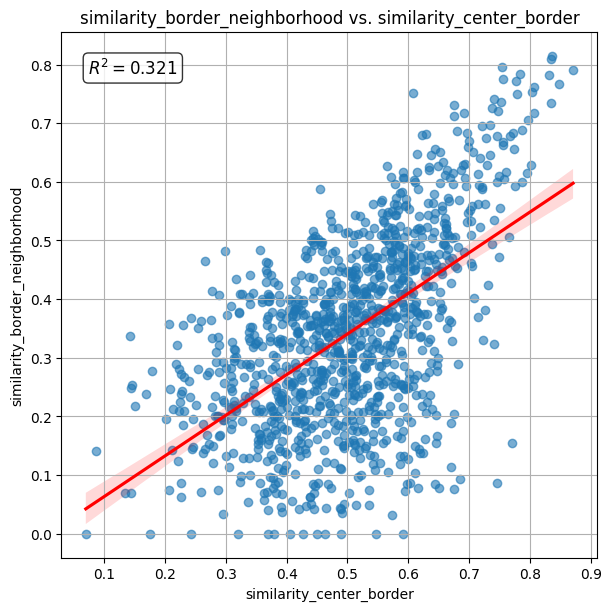
The scatter plot below visualizes the cosine similarity between the cell border and its neigbhorhood plotted against the cosine simiarity between the cell border and cell center. The calculated R2 (coefficient of determination) value is 0.323.
[28]:
plot_regression(
df=sdata["table"].obs,
x="similarity_center_border",
y="similarity_border_neighborhood",
)
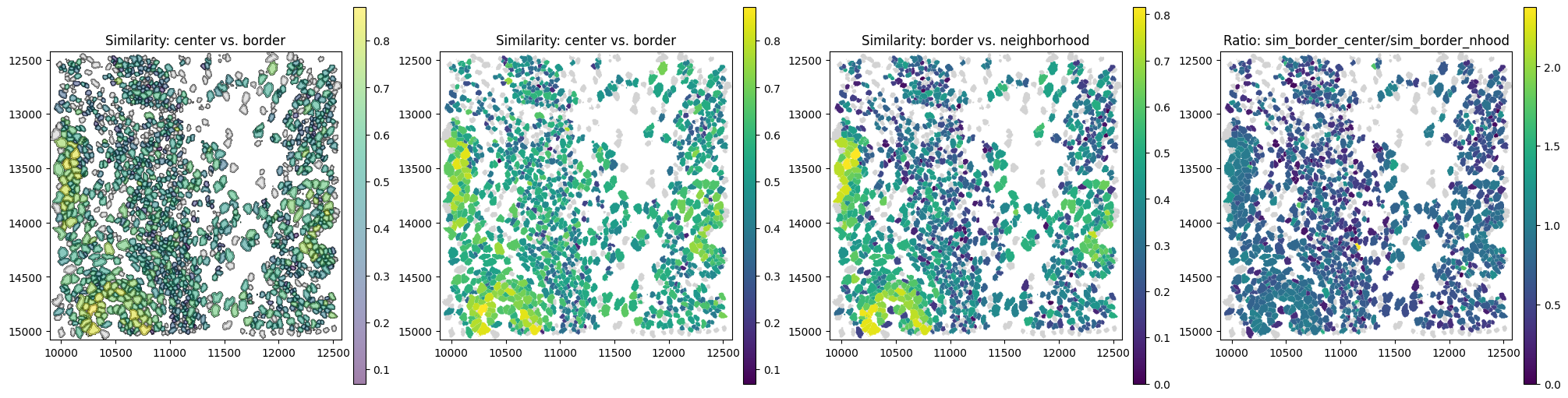
The spatial plots below shows the spatial distribution of computed correlations.
[29]:
# link annotations with cell boundaries
sdata.tables["table"].obs["region"] = "cell_boundaries"
sdata.set_table_annotates_spatialelement("table", region="cell_boundaries")
axes = plt.subplots(1, 4, figsize=(20, 5), constrained_layout=True)[1].flatten()
sdata.pl.render_shapes(
element="cell_centers",
fill_alpha=0.2,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.render_shapes(
element="cell_boundaries",
color="similarity_center_border",
cmap="viridis",
fill_alpha=0.5,
outline_alpha=1.0,
outline_width=0.5,
outline_color="black",
).pl.show(
ax=axes[0],
title="Similarity: center vs. border",
colorbar=True,
figsize=(6, 6),
)
sdata.pl.render_shapes("cell_boundaries", color="similarity_center_border").pl.show(
ax=axes[1], title="Similarity: center vs. border", coordinate_systems="global"
)
sdata.pl.render_shapes("cell_boundaries", color="similarity_border_neighborhood").pl.show(
ax=axes[2], title="Similarity: border vs. neighborhood", coordinate_systems="global"
)
sdata.pl.render_shapes("cell_boundaries", color="ratio_border_neighborhood_to_center").pl.show(
ax=axes[3], title="Ratio: sim_border_center/sim_border_nhood", coordinate_systems="global"
)
WARNING Found 409 NaN values in color data. These observations will be colored with the 'na_color'.
WARNING Found 409 NaN values in color data. These observations will be colored with the 'na_color'.
WARNING Found 409 NaN values in color data. These observations will be colored with the 'na_color'.
WARNING Found 409 NaN values in color data. These observations will be colored with the 'na_color'.
Let’s investigate an example cell with one of the highest ratio_border_neighborhood_to_center.
[30]:
obs = sdata.tables["table"].obs
cid = obs.sort_values("ratio_border_neighborhood_to_center", ascending=False).iloc[0]["cell"]
cid
[30]:
np.uint32(71173)
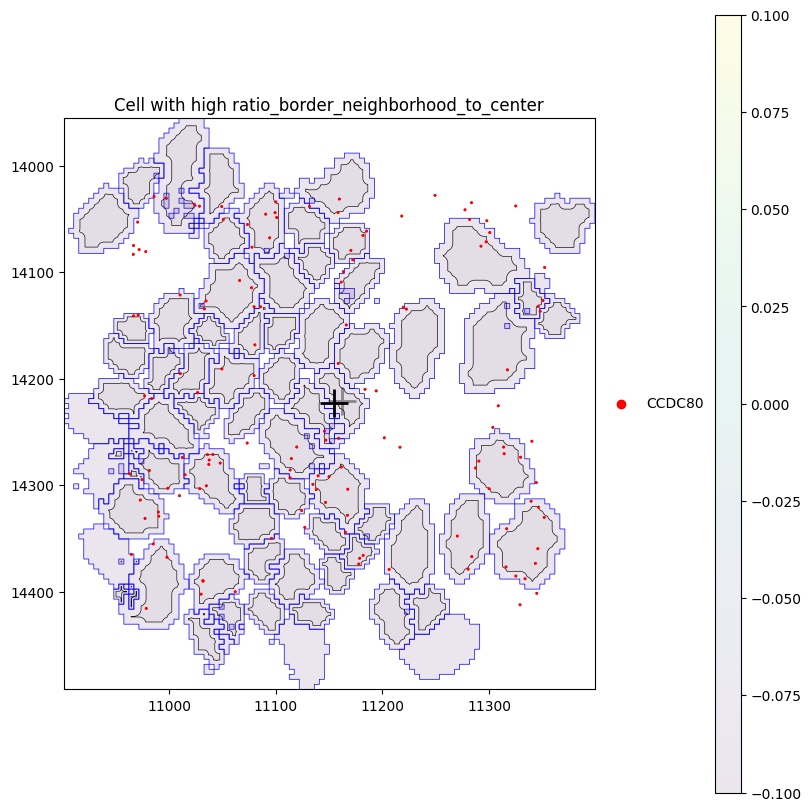
We select one of the most highly abundant genes in this cell, CCDC80. The plot below shows that CCDC80 is distributed across the cell (yellow) border and its neighborhood, but absent from the cell center.
[31]:
tx = sdata.points["transcripts"].compute()
tx.loc[tx["assignment"] == cid, "gene"].value_counts()
[31]:
gene
CCDC80 5
POSTN 5
MRC1 4
FGL2 3
FBLN1 3
..
KLRF1 0
MPO 0
CD79B 0
PDCD1LG2 0
CD3G 0
Name: count, Length: 480, dtype: int64
[32]:
plot_cell_with_nucleus_and_transcripts(
cid,
title="Cell with high ratio_border_neighborhood_to_center",
center_layer="cell_centers",
outer_layer="cell_boundaries",
repositioned_transcripts=True,
genes=["CCDC80"],
)
INFO input has more than 103 categories. Uniform 'grey' color will be used for all categories.
All of the metrics are also stored in the spatialdata object.
[33]:
sdata.tables["table"]
[33]:
AnnData object with n_obs × n_vars = 1533 × 480
obs: 'cell', 'original_cell_id', 'centroid_x', 'centroid_y', 'centroid_z', 'component', 'volume', 'surface_area', 'scale', 'region', 'cell_area', 'similarity_nucleus_cell', 'focal_cell', 'n_outside_cell_all_genes', 'n_in_nucleus_overlap_all_genes', 'n_in_cytoplasm_all_genes', 'pct_outside_cell_all_genes', 'pct_nucleus_all_genes', 'pct_cytoplasm_all_genes', 'nucleus_id', 'iou', 'nucleus_fraction', 'similarity_nucleus_cytoplasm', 'similarity_center_border', 'similarity_border_neighborhood', 'ratio_border_neighborhood_to_center'
var: 'gene', 'total_count', 'lambda_bg_0', 'lambda_bg_1', 'lambda_bg_2', 'lambda_bg_3'
uns: 'spatialdata_attrs', 'proseg_run'
obsm: 'spatial'
obsp: 'transition_counts'
Session Info#
[34]:
print(sd.__version__) # spatialdata
print(spatialdata_plot.__version__)
0.7.2
0.2.13
